House Prices Prediction
Real Estate Economics Meets Machine Learning. In my first Kaggle competition, I combined hedonic pricing theory with modern ML techniques, achieving top 8.1% performance (rank 476/5,887) within 3 days. The approach demonstrated that grounding ML in domain theory provides a clear roadmap for feature engineering, reducing the need for extensive trial-and-error experimentation.
Key Results
Performance
- Average prediction error: ~11.8%(Log-RMSE: 0.111909)
- Final Feature Count: 254 features
- Ensemble Architecture: 8-model hybrid with 2-level stacking
Methodology
- 2-level stacking with Ridge meta-model for optimal model combination
- Theory-driven feature engineering based on hedonic pricing principles
- Domain-aware missing value imputation treating structural absence vs. unknown data
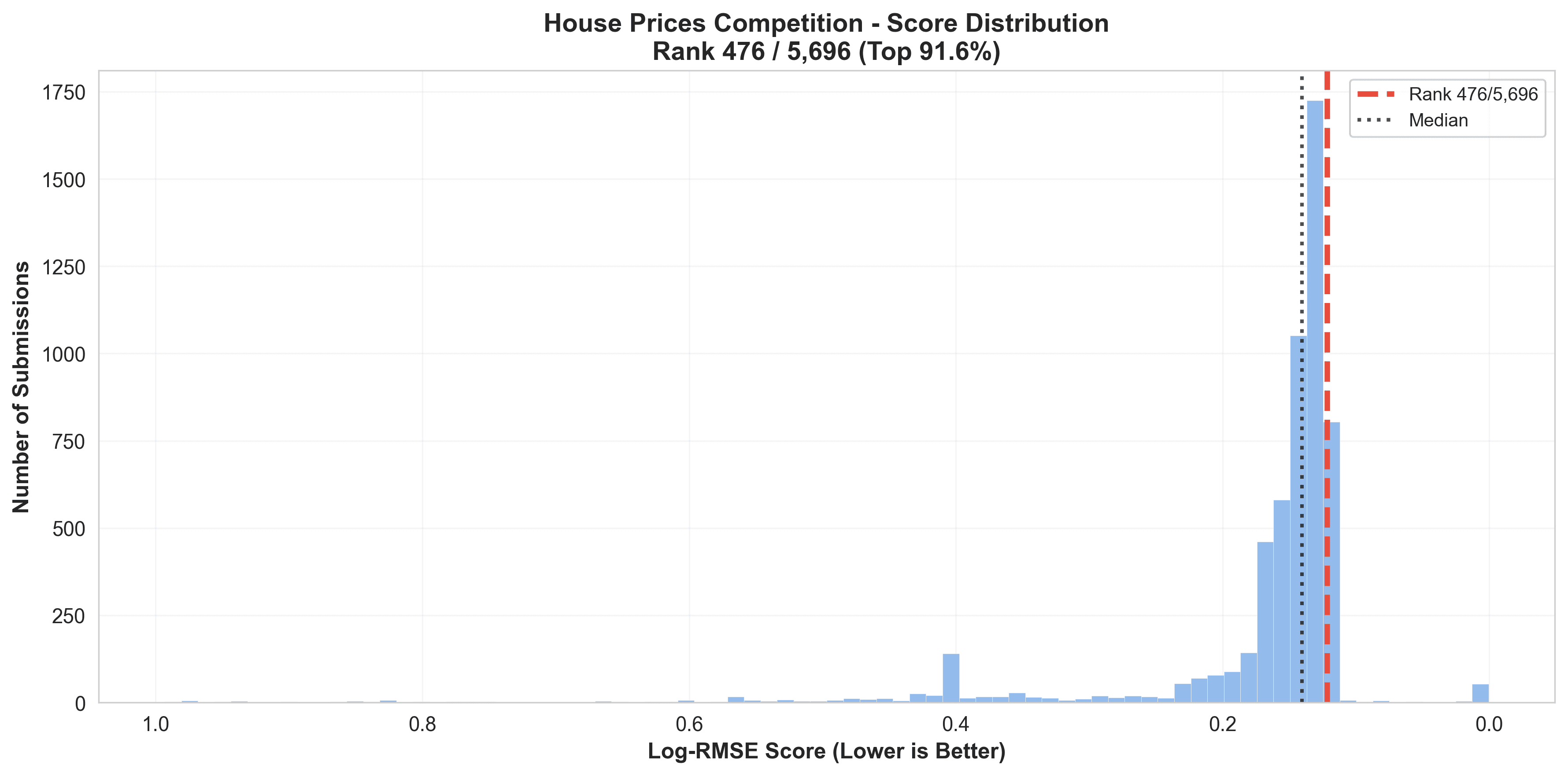
Competition Performance
Leaderboard visualization showing the ensemble's performance across different model combinations and stacking strategies. The final hybrid ensemble achieved optimal balance between bias and variance.
Theoretical Foundation
Hedonic Pricing Theory
A house is a bundle of attributes. The price is the sum of the implicit values of each attribute.
P = f(S, T) where S = Structural attributes (size, rooms, quality) and T = Locational attributes (neighborhood, externalities, lot configuration).
Feature Engineering Principles
- Log transforms for diminishing marginal utility
- Composite features for hedonic pricing
- Spatial equilibrium via neighborhood encoding
- Domain-aware missing value handling
Ensemble Architecture
The solution uses a disciplined 2-level stacking approachcombining 8 diverse models to capture different aspects of the hedonic pricing function.
Level 1: Base Models (8 models)
- Linear Models: Ridge, LASSO, ElasticNet, BayesianRidge, KernelRidge
- Tree-based Models: XGBoost, LightGBM, CatBoost, GradientBoosting
Each model captures different aspects of the hedonic pricing function - linear models approximate the additive attribute values, while tree models capture complex interactions between structural and locational attributes.
Level 2: Meta-Model
Ridge regression (alpha=2) trained on out-of-fold predictions. This simple meta-model prevents overfitting while learning optimal combinations of base model outputs.
Final Blend
Weighted combination of Level 2 stacking output, tree-based model average, and linear model average. This hybrid approach balances the complementary strengths of different model families.
Full Notebook & Code
Explore the complete implementation, methodology, and experimental results on Kaggle. The notebook includes detailed explanations of theory-driven feature engineering, ensemble architecture, and performance analysis.
View on Kaggle